Chain Dimensions
Packing Model & Universal Power Laws

In both the melt state and in a theta-solvent, linear flexible polymer chains follow Gaussian statistics, meaning the average conformation can be described as a random walk in three dimensions. As has been shown by Fetters, Lohse et al., the conformational properties of such chains can be linked to the viscoelastic properties by a single parameter, the so called packing length p.^1,2 This parameter is a measure for the relative thickness of a polymer chain. It is defined as the occupied volume of a chain V_c divided by its mean-square unperturbed end-to-end distance ⟨R²₀⟩:

p = M / [⟨R²₀⟩ ρ N_a] = V_c / ⟨R²₀⟩

where M denotes the molecular weight of the polymer, ρ its melt-state density, and N_a the Avogadro number. V_c is equal to M/(ρN_a). Polymers with a large packing length p exhibit lower elastic energy per chain because larger packing length p means fewer entanglements per chain which results in faster disentanglement at strain and thus in a lower modulus.
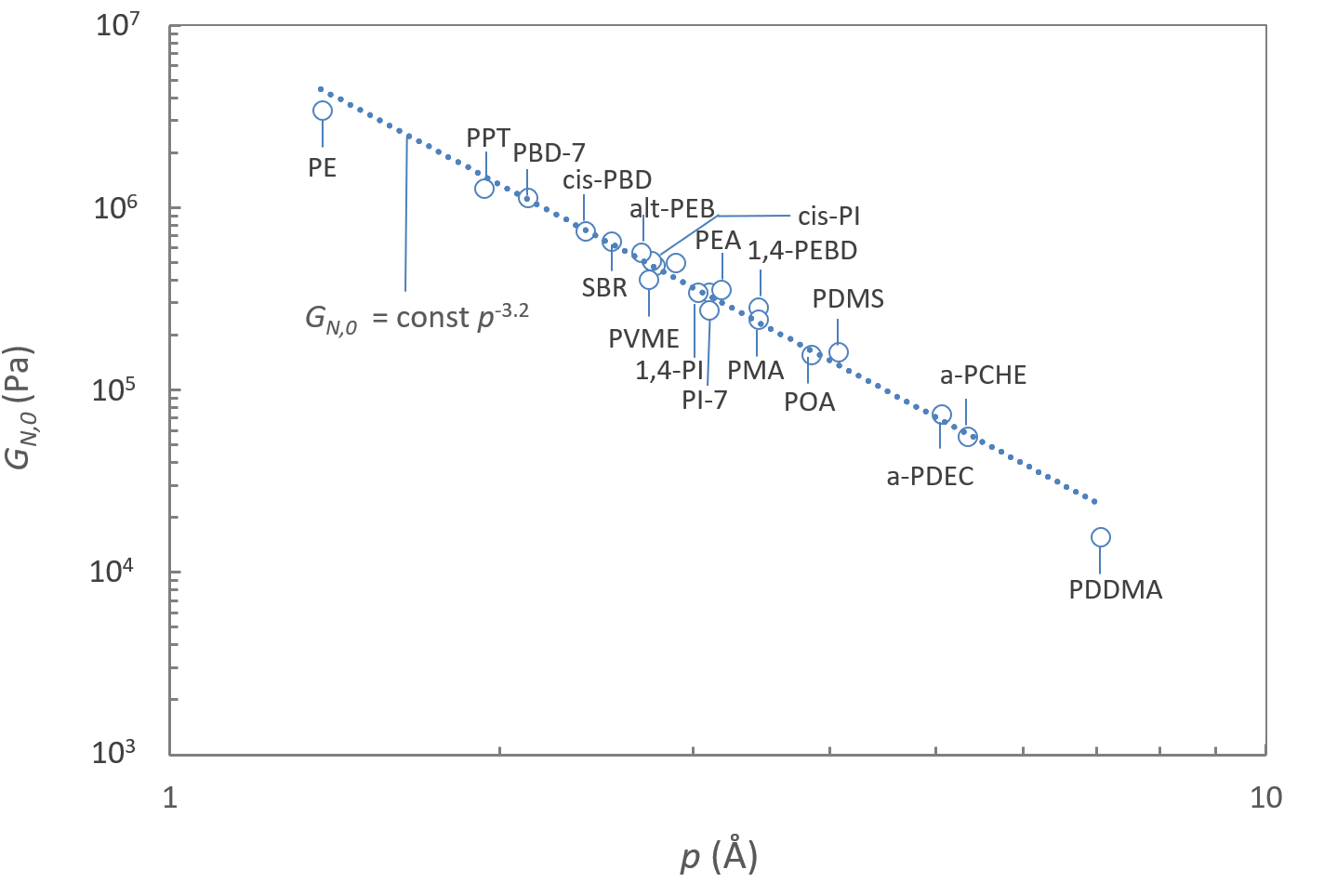
As Fetters et al. have shown, many viscoelastic properties of linear polymers can be described by universal power laws of the form G(p) ∼ pⁿ . For example, they found following power law for the plateau modulus G_N,0 :⁴

G_N,0 = kT / [n_t²p³]

where k denotes the Boltzman constant (k = 1.38 10^-23 J/K), T the temperature, ρ  the polymer melt density and n_t the number of entanglement strands in a volume with dimensions equal to the diameter of the corresponding reptation tube. Thus, a double logarithmic plot of p against G_N,0 (or a linear plot of p^-3 against G_N,0) should yield a straight line, as it is the case for many linear polymers (see figure below).

 

As has been shown by Ferry et al., the rubbery plateau modulus, G_N,0, is inversely proportional to the molecular weight between two successive entanglements:³

G_N,0 = 4/5 · ρ R T / M_e

Combining the two expressions for G_N,0 leads to following power law dependency of the entanglement weight on packing length, entanglement strand density, and melt density:⁴

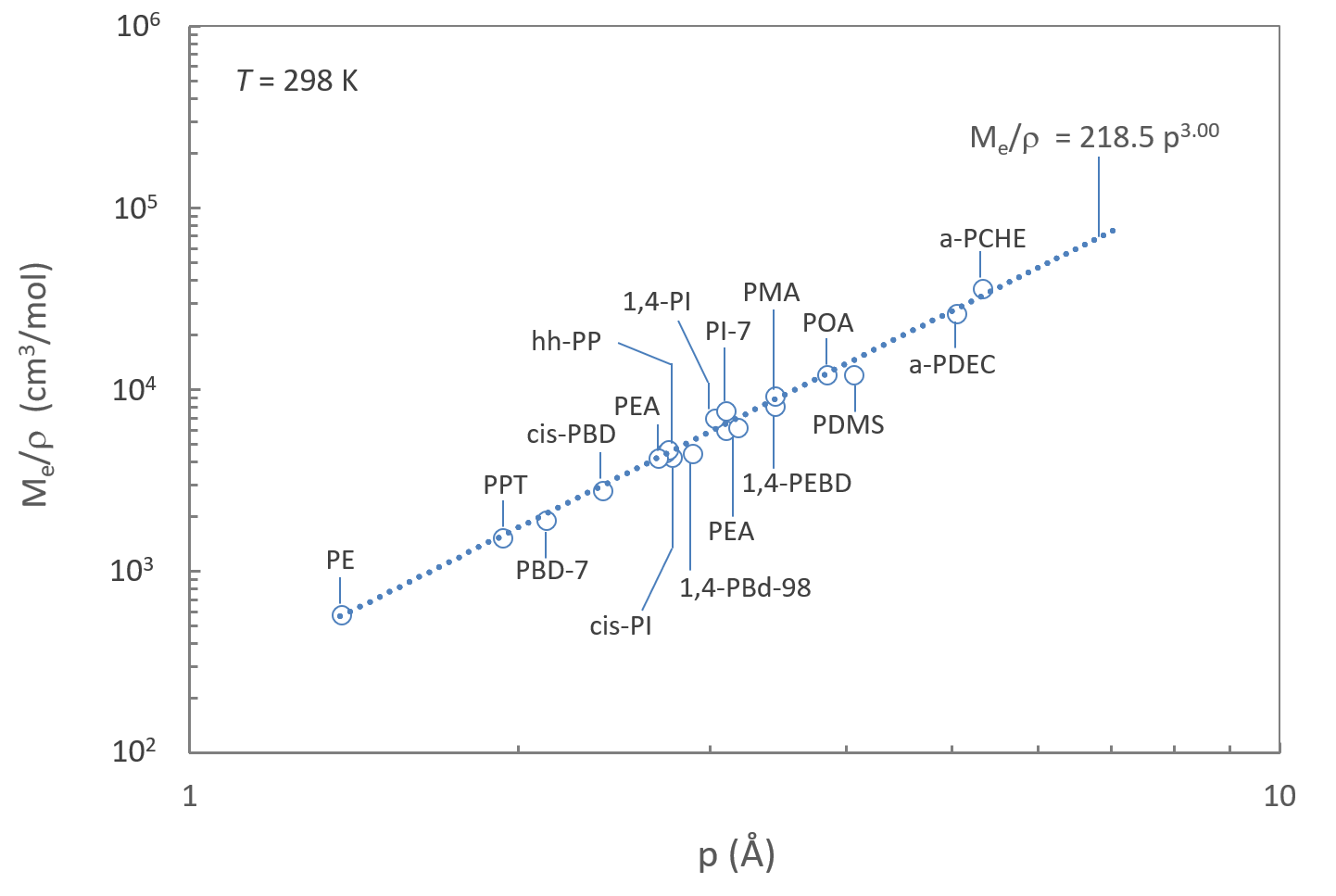
M_e = ρ N_a n_t²p³

Thus the entanglement molecular weight of any linear polymer can be effectively calculated when the conformational properties such as the occupied volume of the polymer chain V_c and its root-mean-square unperturbed end-to-end distance 〈R²₀〉 are known. This finding is not surprising, since ⟨R²₀⟩ is directly related to the entanglement density ν_e.⁵

The Figure below shows a plot of M_e/ρ versus p for a number of polymers (see attached Table). The fitted curve is in good agreement with the scaling law.

 

It is also in excellent agreement with the result of Fetters, Lohse and Graessley who found following equation for polyolefins studied in their work:^4,6,7

M_e/ρ = 361.9 (+/- 31.4) N_a p³ = 218 p³ (298K)

References and Notes

1. L.J. Fetters, D.J. Lohse, D. Richter, T.A. Witten, A. Zirkel, Macromolecules, 27, 4639 (1994)
2. T.A. Witten, S.T. Milner, Z.-G. Wang, in Multiphase Macromolecular Systems, B.M. Culbertson, Plenum Publ. Corp.: New York (1989)
3. J.D. Ferry, Viscoelastic Properties of Polymers, 3rd Ed., John Wiley, New York 1980
4. R. Krishnamoorti et al., J. Poly. Sci.: Part B: Poly. Phys., 40, 1768–1776 (2002)
5. Sougheng Wu, Polymer International 29, 229-247 (1992)
6. L.J. Fetters, D.J. Lohse, W.W., Graessley, J. of Poly. Sci.: Part B: Polymer Physics, Vol. 37, 1023–1033 (1999)
7. The prefactor of 362 is equal to n_t².